# Defining a function to finf the next word using greedy search
def greedy_search(input_text, input_ids, time_steps):
"""
Predict next word using Greedy Search.
Args:
input_text (str): Input text Sequence.
input_ids (torch.Tensor): Input Tensor containing tensorized text sequence
time_steps (int): Number of next steps to predict
"""
iterations = []
with torch.no_grad():
for _ in range(time_steps):
iteration = dict()
iteration['input'] = tokenizer.decode(input_ids[0])
# Predicting using model
output = model(input_ids = input_ids)
next_token_logits = output.logits[0,-1,:]
next_token_probability = torch.softmax(next_token_logits, dim=-1)
sorted_index_of_next_probability = torch.argsort(next_token_probability, descending=True, dim=-1)
# Appending predicted next token to input
input_ids = torch.cat([input_ids, sorted_index_of_next_probability[None, 0, None]], dim=-1)
# Returning iterations as df
return tokenizer.decode(input_ids[0])Intorduction
Have you ever wondered how your phone magically suggests the next word as you type? Or how chatbots string together coherent sentences? The secret lies in something called next token generation.
Think of it this way: imagine telling a story one word at a time. After saying “The big,” what might come next? Perhaps “dog,” “house,” or “tree.” Next token generation teaches computers to do exactly this — predict the most likely word (or sometimes a piece of a word, called a “token”) that should follow the current sequence.
For instance, if you type “Thank you for your,” a next token generation model might suggest “help” as the most likely next word. It’s like having a super-smart autocomplete feature!
In this blog, we’ll pull back the curtain to explore the fascinating techniques behind this technology. We’ll dive into some code to see how it works and compare our results with the leading transformer libraries.
Get ready to explore the world of language prediction, where we’ll examine five popular methods that make next token generation possible: Greedy Search, Beam Search, Top-k Sampling, Top-p (Nucleus) Sampling, and Temperature Control. By the end, you’ll understand how machines learn to speak our language!
In this blog, we’ll use the gpt2-medium model to predict token probabilities, though you’re welcome to experiment with other models.
Greedy Search
When we pass text to a language model and ask it to predict the next word, it calculates the probability of each possible token given the input. The most natural and intuitive approach is to choose the token with the highest probability. This method of choosing the next token is called Greedy Search.
In probabilistic terms, the t th token, given the tokens from 1 to t-1, will be
P\big(W_t|W_{1:t-1}\big) = \argmax_{i} \bigg[P\big(W_i|W_{1:t-1}\big)\bigg]
Let’s see how to implement this. First install torch, transformers, and hf_xet.
Next, let’s import the required libraries, set up our device, and download the model.
Now let’s define a custom function that predicts the next token using greedy search. In this function, we first predict the logits score for each token, then convert those to probabilities using the softmax function.
Let us pass i love and predict next few word using our custom function and compare the result with transformers library.
The output of our custom greedy_search() is
Let’s predicted tokens using transformers library.
Output of transformer library is
Generated words are exactly same hah!!
Since this is an deterministic approach predicted words are exactly same.
If you want to find out what are the other probable tokens and what is there probability you can try this code.
# Defining a function to finf the next word using greedy search
def greedy_search(input_text, input_ids, time_steps, choices_per_step):
"""
Predict next word using greedy Search.
Args:
input_text (str): Input text Sequence.
input_ids (torch.Tensor): Input Tensor containing tensorized text sequence
time_steps (int): Number of next steps to predict
choices_per_step (int): Number of choice at each step.
"""
iterations = []
with torch.no_grad():
for _ in range(time_steps):
iteration = dict()
iteration['input'] = tokenizer.decode(input_ids[0])
# Predicting using model
output = model(input_ids = input_ids)
next_token_logits = output.logits[0,-1,:]
next_token_probability = torch.softmax(next_token_logits, dim=-1)
sorted_index_of_next_probability = torch.argsort(next_token_probability, descending=True, dim=-1)
# Top few highest tokens
for choics_idx in range(choices_per_step):
token_index_sorted = sorted_index_of_next_probability[choics_idx]
token_prob = next_token_probability[token_index_sorted].cpu().numpy()
token_choice = f"{tokenizer.decode(token_index_sorted)} ({token_prob*100:.2f}%)"
iteration[f'Choice {choics_idx+1}'] = token_choice
# Appending predicted next token to input
input_ids = torch.cat([input_ids, sorted_index_of_next_probability[None, 0, None]], dim=-1)
iterations.append(iteration)
# Returning iterations as df
return pd.DataFrame(iterations)Beam Search
One of the main disadvantage of Greedy Search is, it fails to find out high probable words hidden behind low probability word. To fix this, there’s a smarter method called Beam Search. Beam Search doesn’t just pick one word at a time—it keeps track of a few possible paths and explores them to find the best combination of words.
Let’s see how it works with an easy example:
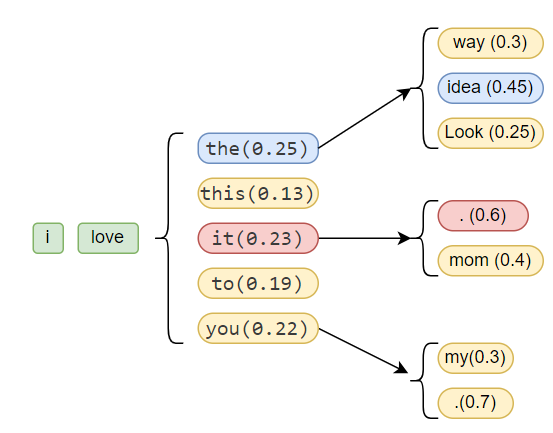
In the preceding example, we’ve considered the initial tokens i and love The model predicts five potential next tokens, with the exhibiting the highest probability. Consequently, a Greedy search strategy would select the as the subsequent token, followed by the token with the highest probability given the, which in this case is idea.
But in Beam search for 2 beams we will be calculating conditional probability of next 2 tokens. The conditional probabilities are:
P('it','.'|'i','love')=0.23\times0.6=0.138
P('it','mom'|'i','love')=0.23\times0.4=0.092
We can observe, the conditional probability of the sequence it and . is the highest among the considered pairs. Therefore, in Beam Search with a beam width of 2, it will be selected as the first subsequent token, rather than the, despite the having the highest individual probability in the previous step.
Let’s try to write a function for beam search
# Beam search function
def beam_search(input_text, max_length=50, num_beams=5):
"""
Predict next word using Beam Search.
Args:
input_text (str): Input text Sequence.
max_length (int): Number of next token to predict.
num_beams (int): Number of Beams to consider.
"""
model.eval()
# Tokenize input and move to device
input_ids = tokenizer.encode(prompt, return_tensors="pt").to(device)
# Initialize beams: Each beam starts with the same initial input
beams = [(input_ids, 0)] # Tuple of (tokens, score)
for _ in range(max_length):
new_beams = []
for tokens, score in beams:
# Get model predictions
with torch.no_grad():
outputs = model(tokens)
# Extract logits for the last token and apply softmax
logits = outputs.logits[:, -1, :]
probs = torch.softmax(logits, dim=-1)
# Get top beam candidates
top_probs, top_indices = probs.topk(num_beams)
# Create new beams
for i in range(num_beams):
new_token = top_indices[:, i].unsqueeze(-1)
new_score = score + torch.log(top_probs[:, i]) # Update score
new_beam = (torch.cat([tokens, new_token], dim=-1), new_score)
new_beams.append(new_beam)
# Sort beams by score and keep the best ones
new_beams.sort(key=lambda x: x[1], reverse=True)
beams = new_beams[:num_beams]
# Select the best final beam
best_tokens = beams[0][0]
return tokenizer.decode(best_tokens[0], skip_special_tokens=True)Let’s Try with the same input i love and then try to generate next 2 tokens using beam_search() function:
# Example usage
input_text = "i love"
generated_text = beam_search(input_text, max_length=10, num_beams=2) # num_beams = 1 is same as greedy search
print(generated_text)One thing to note, Beam Search with one beam is same as greedy search.(Verify!)
Now Let’s us compare the result form our function and output from transformers library.
input_text = "i love"
# Input Tokens
input_tokens = tokenizer(input_text, return_tensors= 'pt').to(device)
# Generating data from model using Hugging face library
output = model.generate(**input_tokens, max_new_tokens=10, num_beams = 3)
print(tokenizer.decode(output[0], skip_special_tokens= True))Interestingly, the outputs in both scenarios end up being identical. However, a noticeable issue is the repetitiveness of the generated text. This tendency towards repetition is a common drawback of deterministic decoding strategies. To mitigate this, we can introduce an element of randomness into the token selection process.
Top-k Search
To introduce randomness into the token selection process, one effective method is to randomly choose a token from the top k most probable predictions. This technique is known as Top-k Sampling or Top-k Search. The process involves the following steps:
- Predict Probabilities: First, the model predicts the probability distribution over all possible tokens.
- Select Top-k: We then identify and select the k tokens with the highest probabilities.
- Normalize Probabilities: The probabilities of these k selected tokens are re-normalized to create a new probability distribution.
- Random Selection: Finally, a token is randomly chosen from this renormalized distribution.
Let’s illustrate this with a Python function:
def top_k_search(input_text, max_length=50, k=5, show_option= False):
"""
Predict next word using top k Search.
Args:
input_text (str): Input text Sequence.
max_length (int): Number of next token to predict.
k (int): Number of high probability token to consider.
show_option (bool): If true shows top k tokens at each step.
"""
model.eval()
# Tokenize input and move to device
input_ids = tokenizer.encode(input_text, return_tensors="pt").to(device)
# output_tokens
output_tokens = input_ids
for _ in range(max_length):
if show_option:
print(f"\nFor {_+1} Token:")
print("-"*100)
# Get model predictions
with torch.no_grad():
outputs = model(output_tokens)
# Extract logits for the last token and apply softmax
logits = outputs.logits[:, -1, :]
probs = torch.softmax(logits, dim=-1)
# Get top beam candidates
top_probs, top_indices = probs.topk(k)
# Normalizing top K probabilities
top_probs_norm = top_probs/torch.sum(top_probs)
# Choosing an element randomly based on normalized probability of top k tokens
selected_token_id = torch.multinomial(top_probs_norm[0], num_samples=1, replacement= True)
selected_token = top_indices[0][selected_token_id.item()]
# Reshape selected_token to have shape (1, 1)
selected_token = selected_token.unsqueeze(0).unsqueeze(0) # This will reshape selected token to (1,1) and will solve the error.
# Appending selected token with input token
output_tokens = torch.cat((output_tokens, selected_token), dim=1)
if show_option:
# Printing Top K tokens
print(f"Selected Token: {tokenizer.decode(selected_token.item())}\nTop K tokens are:\n")
for index, probability in zip(top_indices.squeeze(0), top_probs_norm.squeeze(0)):
print(f"{tokenizer.decode(index.item())} ({round(probability.item() * 100, 2)}%)")
return tokenizer.decode(output_tokens[0], skip_special_tokens=True) # decode function works on 1D array only.
# Example usage
input_text = "i love"
generated_text = top_k_search(input_text, max_length=1, k=5, show_option = True) # num_beams = 1 is same as gready search
print("-"*20 + "\nFinal generated Text is:\n" + generated_text + "\n" + "-"*20)Top 5 most probable tokens are:
For 1 Token:
----------------------------------------------------------------------------------------------------
Selected Token: the
Top K tokens are:
the (22.54%)
it (22.47%)
you (21.72%)
to (19.86%)
this (13.4%)The next selected token is the. At this step, the five most probable predicted tokens are the, it, you, to, and this. From these five, one token will be randomly selected based on their respective probabilities.
The subsequent words were generated using the transformers library.
# set seed to reproduce results. Feel free to change the seed though to get different results
from transformers import set_seed
input_text = "i love"
# Input Tokens
input_tokens = tokenizer(input_text, return_tensors= 'pt').to(device)
# set top_k to 50
sample_output = model.generate(
**input_tokens,
max_new_tokens=4,
do_sample=True,
top_k=5
)
print("Output:\n" + 100 * '-')
print(tokenizer.decode(sample_output[0], skip_special_tokens=True))In this instance, the predicted token is also the, although this is purely coincidental. Rerunning the code might yield a different token, but it’s important to note that the subsequent selected token will invariably be one of the five most probable tokens from the preceding output (as you can verify!).
input_text = "i love"
generated_text = top_k_search(input_text, max_length=10, k=5)
print("-"*20 + "\nFinal generated Text is:\n" + generated_text + "\n" + "-"*20)--------------------
Final generated Text is:
i love the way he's doing this, but I'm
--------------------If we predict next 10 tokens we can see there is not any repetition to tokens like previous case.
Top-p Search
Another effective method involves considering a dynamic set of the most probable tokens whose cumulative probability exceeds a predefined threshold, p. This technique is known as Top-p Sampling or Nucleus Sampling.
The process unfolds as follows:
- Predict Probabilities: Initially, the model predicts the probability distribution over all possible tokens.
- Identify the Nucleus: We then identify the smallest set of most probable tokens such that the sum of their probabilities is greater than or equal to the probability threshold p.
- Normalize Probabilities: The probabilities of the tokens within this selected set (the “nucleus”) are renormalized to create a new probability distribution.
- Random Selection: Finally, a token is randomly chosen from this renormalized distribution.
Let’s illustrate this with a Python function:
def top_p_search(input_text, max_length=50, p=1, show_option= False):
"""
Predict next word using top p Search.
Args:
input_text (str): Input text Sequence.
max_length (int): Number of next token to predict.
p (float): Probability Threshold.
show_option (bool): If true shows top k tokens at each step.
"""
model.eval()
# Tokenize input and move to device
input_ids = tokenizer.encode(input_text, return_tensors="pt").to(device)
# output_tokens
output_tokens = input_ids
for _ in range(max_length):
if show_option:
print(f"\nFor {_+1} Token:")
print("-"*100)
# Get model predictions
with torch.no_grad():
outputs = model(output_tokens)
# Extract logits for the last token and apply softmax
logits = outputs.logits[:, -1, :]
probs = torch.softmax(logits, dim=-1)
# Get top beam candidates
probs, indices = torch.sort(probs, dim = 1, descending=True)
cumulative_prob = torch.cumsum(probs[0], dim = 0)
top_probs = probs[:,:torch.sum(cumulative_prob<=p).item() + 1]
top_indices = indices[:,:torch.sum(cumulative_prob<=p).item() + 1]
# Normalizing top K probabilities
top_probs_norm = top_probs/torch.sum(top_probs)
# Choosing an element randomly based on normalized probability of top k tokens
selected_token_id = torch.multinomial(top_probs_norm[0], num_samples=1, replacement= True)
selected_token = top_indices[0][selected_token_id.item()]
# Reshape selected_token to have shape (1, 1)
selected_token = selected_token.unsqueeze(0).unsqueeze(0) # This will reshape selected token to (1,1) and will solve the error.
# Appending selected token with input token
output_tokens = torch.cat((output_tokens, selected_token), dim=1)
if show_option:
# Printing Top K tokens
print(f"Selected Token: {tokenizer.decode(selected_token.item())}\nTop K tokens are:\n")
for index, probability in zip(top_indices.squeeze(0), top_probs_norm.squeeze(0)):
print(f"{tokenizer.decode(index.item())} ({round(probability.item() * 100, 2)}%)")
return tokenizer.decode(output_tokens[0], skip_special_tokens=True) # decode function works on 1D array only.
# Example usage
input_text = "i love"
generated_text = top_p_search(input_text, max_length=1, p=0.5, show_option= True)
print("-"*20 + "\nFinal generated Text is:\n" + generated_text + "\n" + "-"*20)For 1 Token:
----------------------------------------------------------------------------------------------------
Selected Token: the
Top K tokens are:
the (17.06%)
it (17.01%)
you (16.44%)
to (15.03%)
this (10.14%)
that (7.91%)
my (5.68%)
her (3.64%)
him (3.56%)
them (3.53%)
--------------------
Final generated Text is:
i love the
--------------------with p=0.5 when we predict next token there are 10 possible tokens. Out of then token the has been selected. You can rerun the code and verify weather your predicted token is out of these 10 tokens or not.
Temperature
Introducing randomness alone isn’t always sufficient for generating desired text. When the goal is to extract and present information based on a specific document, prioritizing tokens with the highest probability is often preferred for accuracy and coherence. However, when crafting creative content like blog posts, encouraging the model to explore more diverse and unexpected word choices can lead to richer and more engaging outputs.
This balance between predictability and creativity can be effectively controlled using a parameter called temperature. The temperature value adjusts the probability distribution of the predicted tokens. A low temperature makes the distribution sharper, increasing the likelihood of selecting high-probability tokens and thus resulting in more focused and deterministic output. Conversely, a high temperature flattens the probability distribution, giving lower-probability tokens a greater chance of being selected, thereby injecting more randomness and creativity into the generated text.
Let’s define a custom softmax function that incorporates this temperature parameter:
import torch.nn.functional as F
# Defining updated softmax for PyTorch tensors
def softmax_tensor(logits: torch.Tensor, temperature: float = 1.0) -> torch.Tensor:
"""
Applies the softmax function to a PyTorch tensor along the last dimension,
optionally with a temperature scaling factor.
Args:
logits: The input PyTorch tensor of logits.
temperature: A scaling factor for the logits (default: 1.0).
Returns:
A PyTorch tensor of the same shape as the input, with probabilities
along the last dimension.
"""
return F.softmax(logits / temperature, dim=-1)Updating Top-p Search function by including temperature parameter.
def top_p_search(prompt, max_length=50, p=1, temperature = 1, show_option = False):
"""
Predict next word using top p Search with temperature.
Args:
input_text (str): Input text Sequence.
max_length (int): Number of next token to predict.
p (float): Probability Threshold.
temperature (float): A number of control randomness.
show_option (bool): If true shows top k tokens at each step.
"""
model.eval()
# Tokenize input and move to device
input_ids = tokenizer.encode(prompt, return_tensors="pt").to(device)
# output_tokens
output_tokens = input_ids
for _ in range(max_length):
if show_option:
print(f"\nFor {_+1} Token:")
print("-"*100)
# Get model predictions
with torch.no_grad():
outputs = model(output_tokens)
# Extract logits for the last token and apply softmax
logits = outputs.logits[:, -1, :]
probs = softmax_tensor(logits= logits, temperature= temperature + 1e-6) # Added temperature while calculating probability
# Get top beam candidates
probs, indices = torch.sort(probs, dim = 1, descending=True)
cumulative_prob = torch.cumsum(probs[0], dim = 0)
top_probs = probs[:,:torch.sum(cumulative_prob<=p).item() + 1]
top_indices = indices[:,:torch.sum(cumulative_prob<=p).item() + 1]
# Normalizing top K probabilities
top_probs_norm = top_probs/torch.sum(top_probs)
# Choosing an element randomly based on normalized probability of top k tokens
selected_token_id = torch.multinomial(top_probs_norm[0], num_samples=1, replacement= True)
selected_token = top_indices[0][selected_token_id.item()]
# Reshape selected_token to have shape (1, 1)
selected_token = selected_token.unsqueeze(0).unsqueeze(0)
# Appending selected token with input token
output_tokens = torch.cat((output_tokens, selected_token), dim=1)
if show_option:
# Printing Top K tokens
print(f"Selected Token: {tokenizer.decode(selected_token.item())}\nTop K tokens are:\n")
for index, probability in zip(top_indices.squeeze(0), top_probs_norm.squeeze(0)):
print(f"{tokenizer.decode(index.item())} ({round(probability.item() * 100, 2)}%)")
return tokenizer.decode(output_tokens[0], skip_special_tokens=True)
# Example usage with very low temperature
input_text = "i love"
generated_text = top_p_search(input_text, max_length=10, p=0.7, temperature=0.1)
print("-"*20 + "\nFinal generated Text is:\n" + generated_text + "\n" + "-"*20)Tokens generated with very low temperature of the model:
--------------------
Final generated Text is:
i love the idea of a "super-hero" who
--------------------Consequently, as you can observe, the initial few tokens closely mirror the results obtained with our earlier deterministic approach. Let’s now explore the effect of increasing the temperature.
input_text = "i love"
generated_text = top_p_search(input_text, max_length=10, p=0.7, temperature=1)
print("-"*20 + "\nFinal generated Text is:\n" + generated_text + "\n" + "-"*20)--------------------
Final generated Text is:
i love you no matter what," Trump wrote in a January
--------------------Upon increasing the temperature to 1, we observe that the model begins to select more varied and less predictable words. However, it’s important to note that employing excessively high temperature values can lead to generated text that lacks coherence and meaning. A generally recommended and effective range for the temperature parameter is between 0 and 1.
input_text = "i love"
generated_text = top_p_search(input_text, max_length=10, p=0.7, temperature=0.7)
print("-"*20 + "\nFinal generated Text is:\n" + generated_text + "\n" + "-"*20)Text generated with temperature 0.7 feel more natural. (Try playing with different temperature value)
You can also see the list of all possible words by changing show_option parameter to True at different temperature value. ( Try playing with that as well, and see if you observe any pattern among the number of words and temperature value.)
A special thank you to Rohan-Paul-AI for the inspiration behind this post, and thanks also to Koushik Khan for encouraging me to write it!